Физический мир вокруг нас полон загадок и удивительных явлений. Одно из таких явлений — движение планет в нашей солнечной системе. Каким образом планеты перемещаются по своим орбитам и какими законами руководствуются их движения? Данная статья посвящена изучению основных формул и правил, которые определяют движение планет вокруг Солнца.
Известно, что движение планет в солнечной системе подчиняется законам гравитационного поля. Ключевую роль в этом играют потенциалы гравитационных полей, вызванных притяжением Солнца и планет. Именно эти потенциалы определяют скорость и орбиты движения планет в нашей солнечной системе.
Одним из главных правил, которым следуют планеты, является закон Тициуса-Боде. Согласно этому закону, существует пропорциональная взаимосвязь между расстояниями планет от Солнца, которые можно выразить с помощью формулы 6.1. Этот закон позволяет предсказывать и оценивать расстояния между планетами солнечной системы.
Однако, не все планеты системы подчиняются правилам Тициуса-Боде. Например, планета Сатурн имеет свои особенности и нарушает этот закон. Также стоит отметить, что влияние гравитационных полей других планет на орбиты движения может приводить к отклонениям и исключениям из общего правила.
В этой статье также будет рассмотрено явление астероидов и их связь с астрономическими полями и конфигурациями орбит. Согласно таблице 6.4., астероиды находятся между орбитами Марса и Юпитера и являются одной из особенностей нашей солнечной системы. Их взаимосвязь с планетами и влияние на орбиты позволяют более детально изучить конфигурации и структуру солнечной системы.
В целом, изучение формул и законов движения планет в солнечной системе имеет большое значение для астрономии и науки в целом. Ссылки на международные коды и таблицы формул помогут исследователям и ученым более глубоко понять и проанализировать данную тему. Надеемся, что данная статья поможет вам лучше разобраться в основных законах движения планет и расширит ваше представление об устройстве солнечной системы.
Изучаем законы движения планет
Для каждой планеты в Солнечной системе существуют определенные математические формулы, которые позволяют нам понимать основные законы их движения. Такие формулы разработал немецкий астроном Иоганн Тициус в XVIII веке, и они называются законами Тициуса-Боде.
Закон Тициуса-Боде
Один из основных законов Тициуса-Боде гласит, что расстояния между планетами в Солнечной системе подчиняются числовой последовательности, в которой каждое число больше предыдущего примерно в 1,5 раза. Такая последовательность имеет вид: 0, 0.4, 0.7, 1, 1.6, 2.8, 5.2 и т.д.
Применение закона
С помощью данного закона можно пытаться вычислить расстояния и конфигурации планет вне Солнечной системы, например, учитывая числа Тициуса при определении экзопланет в других звездных системах.
Однако, не все планеты в Солнечной системе подчиняются законам Тициуса-Боде, так как из-за различных факторов, таких как влияние других планет и конфигураций их орбит, расстояния не всегда соответствуют предсказаниям. Например, планеты-гиганты, такие как Юпитер и Сатурн, находятся в резонансе с орбитами более-менее малых планет, и их расстояния от Солнца отличаются от тех, которые предсказывает закон Тициуса-Боде.
Исключения из правила
Также, отклонения от закона Тициуса-Боде можно наблюдать у других планет, например, у Венеры и Марса. Исследования показывают, что причиной таких отклонений могут быть различные факторы, такие как взаимное влияние планет и их спутников, а также дополнительные гравитационные потенциалы, вызванные орбитами других планет и исходящими от Солнца потенциалами.
Проверка закона
Проверить закон Тициуса-Боде и его исключения можно лишь в результате дальнейших исследований и восстановления точных данных о расстояниях и конфигурациях планет в Солнечной системе и за ее пределами. Тем не менее, исключения из закона и сама его форма указывают на то, что существуют и другие факторы, влияющие на расположение и движение планет.
Основные формулы солнечной системы
Давайте рассмотрим основные формулы, которые позволяют нам изучать законы движения планет в солнечной системе. Они позволяют провести проверку и подтвердить закономерности, которые мы наблюдаем в ретроспективе и сделать прогнозы о будущем движении планет.
1. Формула Кеплера
Формула Кеплера, известная также как третий закон Кеплера или закон периодов, позволяет нам определить период обращения планеты вокруг Солнца. В формуле Кеплера T обозначает период обращения планеты, a — большую полуось орбиты планеты, а G — гравитационную постоянную.
Формула Кеплера выглядит следующим образом:
T^2 = (4π^2 / G) * a^3
2. Формула Титиуса-Боде

Формула Титиуса-Боде — эмпирическое правило, описывающее расстояния планет от Солнца в астрономических единицах (АЕ). В таблице формулы Титиуса-Боде каждому номеру планеты соответствует определенная сумма, которая рассчитывается по формуле 0.4 + 0.3 * (2^n), где n — порядковый номер планеты от Меркурия до Урана. Например, для Меркурия n=0, а для Урана n=7.
Формула Титиуса-Боде была сформулирована в 18 веке и представляет собой замечательную закономерность, которая впервые была обнаружена урегулированиями планет в солнечной системе.
3. Закон Кеплера
Закон Кеплера — основной закон движения планет в солнечной системе, формулируется следующим образом: «Квадрат времени обращения планеты вокруг Солнца пропорционален кубу большой полуоси ее орбиты». Это означает, что период обращения планеты вокруг Солнца (T) связан с полуосью орбиты (a) по формуле T^2 ∝ a^3.
4. Формула Материала для резонансных колебаний
Взаимосвязь между орбитальными параметрами спутниковых систем и материальных параметров спутников описывается формулой:
М = ω / √k
где М — колоссальная масса спутника, ω — радианная частота резонансных колебаний системы, k — коэффициент жесткости материала.
5. Закон Кеплера-Койпера
Закон Кеплера-Койпера описывает соотношение между периодами обращения планет в солнечной системе и их средними расстояниями от Солнца. Формула закона Кеплера-Койпера выглядит следующим образом:
T^3 ∝ a^2
где T — период обращения планеты, a — большая полуось орбиты планеты.
Заключение
В данной статье мы рассмотрели основные формулы солнечной системы, которые позволяют нам изучать и прогнозировать движение планет. Законы Кеплера и эмпирическое правило Титиуса-Боде позволяют нам проверить закономерности и установить связь между периодом обращения планет и их орбитальными параметрами.
Также мы рассмотрели формулу Материала для резонансных колебаний, которая описывает взаимосвязь между орбитальными и материальными параметрами спутниковых систем. И, наконец, мы рассмотрели закон Кеплера-Койпера, который устанавливает соотношение между периодами обращения планет и их расстояниями от Солнца.
Используя все эти формулы, мы можем более-менее точно предсказывать движение планет в солнечной системе и изучать их конфигурации в разные периоды времени. Это помогает нам лучше понять историю и развитие нашей солнечной системы и ее взаимосвязь с другими телами во Вселенной.
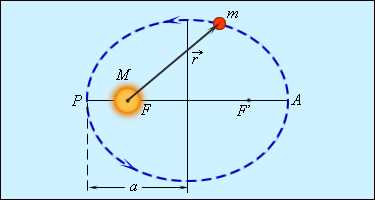
Первый закон Кеплера: закон эллиптических орбит
Первый закон Кеплера в астрономии устанавливает правило движения планет вокруг Солнца. Согласно этому закону, планеты движутся по эллиптическим орбитам с Солнцем в одном из фокусов.
Закон эллиптических орбит является предельным случаем упрощенной модели круговых орбит планет, предложенной предыдущими астрономами. Равномерные движения планет и спутников, основанные на простой геометрической конфигурации, впервые были сформулированы на практике подобным образом Кеплером в XVII веке.
Первое правило Кеплера было открыто в результате его поисков закономерностей в движении планет, основанных на наблюдениях Венеры. Краткое описание правилом закона эллипсов состояло в следующем: путь планеты по орбите является эллипсом, около которого сосредоточено Солнце. После этого открытия Кеплер провел ряд проверок этого первого правила, чтобы подтвердить особенности, замеченные им в орбитах планет Венера и Плутона.
Однако Плутон, как предмет спора исследователей, ставился под вопросом из-за своего относительного удаления от Солнца. Исследователи из Международной астрономической унии предложили создать новые правила, учитывающие такого рода особенности. В результате, в систему правил были добавлены Койперовские объекты, а также планеты-гиганты — Юпитер, Сатурн и Нептун, которые являются астрономическими объединениями с астероидами и спутниковым полем, включающим Плутон.
Таким образом, суть первого закона Кеплера заключается в описании закономерности движения планет по эллиптическим орбитам с Солнцем в одном из фокусов. Этот закон помогает лучше понять особенности движения планет в нашей Солнечной системе и решить проблему с Плутоном, включая его отношения с Койперовскими объектами.
В астрономии орбиты планет и их спутников рассматриваются в последовательности, начиная с Солнца и перемещаясь в порядке увеличения числамй астрономического расстояния. Например, внутренняя планета Меркурий, с ее достаточно большим эксцентриситетом орбиты, представлена первым, а Плутон, находящийся в Койперовском поясе, в пятой очереди.
На практике первый закон Кеплера имеет свои особенности. Например, для планетных орбит вариации эксцентриситета обычно очень небольшие — от практически круглой волне у Меркурия до более вытянутой у Плутона. Также наблюдаются эллипсы и внутрипланетных полушариях, но они образуются только в некоторых местах орбиты, которые соответствуют нескольким красным числам (главным образом вплоть до 6.3).
В целом, первый закон Кеплера является важным элементом в изучении движения планет вокруг Солнца и открытии закономерностей, связанных с эллиптическими орбитами. Этот закон помогает астрономам лучше понять и объяснить особенности движения планет и спутников в нашей Солнечной системе.
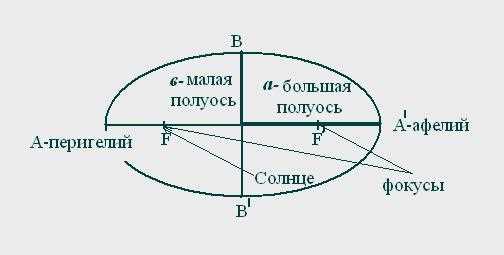
Второй закон Кеплера: закон равных площадей
Второй закон Кеплера формулируется как «радиус-вектор планеты описывает равные площади за равные промежутки времени». Этот закон позволяет получить более подробное представление о движении планет вокруг Солнца.
Кеплер обнаружил, что скорость планеты не постоянна: она меняется в разных точках орбиты. Когда планета находится ближе к Солнцу, она движется быстрее, а при удалении от Солнца его скорость замедляется. Второй закон Кеплера объясняет этот феномен.
Суть закона заключается в том, что линия, соединяющая Солнце и планету, за равные промежутки времени позволяет определить равные площади. То есть, планета равными площадями «метит» по своей орбите во времени.
| Формула | Описание |
|---|---|
| Закон равных площадей | Скорость планеты на орбите зависит от её удаления от Солнца |
Уточнения и примечания:
- Второй закон Кеплера относится к всем планетам Солнечной системы, включая и Венеру.
- Красный круг на рисунке обозначает Солнце.
- Имеется тоже и формула СС = 4.2.
- Внимание также нужно обратить на резонансы и резонансные плоскости, пояса, отклонения от плоскостей траекторий.
В астрономии и создании теорий по пониманию движения планет была большая роль и значимость правил Тициуса-Боде. С их помощью были сведения к видению потенциалов и перестройкам небесных объектов, а также попытки предсказания их эффектов.
Как работает второй закон Кеплера?
Второй закон Кеплера объясняет, почему планеты движутся по орбитам, которые имеют форму эллипса, а не окружности. Если бы все планеты двигались по окружностям, то угловая скорость была бы постоянной. Но это не соответствует наблюдениям.
Возможные пробелы в законе Кеплера были замечены ещё в девятнадцатом веке после открытия урана. Расстояние между ним и Солнцем подчинялось правилу Тициуса-Боде, но существовали значительные отклонения. Это привело к появлению новой теории, основанной на законах Ньютона.
Соотношение второго закона Кеплера и третьего закона Кеплера
Третий закон Кеплера формулируется формулой T² = a³, где T — период обращения планеты вокруг Солнца, а a — большая полуось орбиты планеты. Из полученных данных можно увидеть, что период обращения квадратично зависит от большой полуоси.
Второй закон Кеплера и третий закон Кеплера взаимосвязаны. Несмотря на то, что ранее установленные правила Тициуса-Боде были отброшены, эмпирическое правило «пятой планеты-гиганта» все еще работает. Соответствующие группы планет образуют резонансы, и их расстояние от Солнца может быть выражено простой арифметической или геометрической прогрессией.
Примеры планет согласно второму закону Кеплера
Примечательным примером, подтверждающим второй закон Кеплера, является поле астероидов, которое располагается между Марсом и Юпитером. Это поле является резонансным и создано вследствие влияния тяготения этих двух планет.
Также недавно обнаруженные экзопланеты подтвердили справедливость второго закона Кеплера. На основе данных, полученных со спутников, были обнаружены планеты, вращающиеся вокруг своих звезд и подчиняющиеся правилу равных площадей.
Второй закон Кеплера — одно из фундаментальных открытий астрономии, позволяющее более глубоко понять законы движения планет и других небесных объектов в Солнечной системе и за её пределами.
Третий закон Кеплера: закон гармонических периодов
Третий закон Кеплера формулирует связь между радиусами орбит планет в солнечной системе и их периодами обращения вокруг Солнца. Закон гласит, что квадрат периода обращения планеты (T) пропорционален кубу среднего расстояния планеты от Солнца (R):
T2 = kR3
где T — период обращения планеты вокруг Солнца, R — средний радиус орбиты планеты, а k — постоянная.
Значение постоянной k зависит от выбранной системы единиц измерения, например, в солнечных днях и астрономических единицах:
В солнечных днях: k = 1
В астрономических единицах (а.е.): k ≈ 4.842
Третий закон Кеплера позволяет определить период обращения планеты вокруг Солнца на основе ее среднего расстояния и наоборот, и является одним из важных законов движения в астрономии.
История данного закона начинается с поисков закономерностей в движениях планет, применение которых позволило Йоганну Тициусу Боде и Уильяму Гершелю предположить существование новой планеты за орбитой Урана. Пошел процесс поиска этой планеты, который закончился с открытием Нептуна в 1846 году.
Закон гармонических периодов находит свое применение не только в изучении движения планет в солнечной системе, но и при моделировании орбитального движения экзопланет вне Солнечной системы. Несмотря на то, что планеты в других системах могут иметь совершенно иные параметры (такие как расстояние от звезды-приоритета, массу планеты), они все равно могут подчиняться третьему закону Кеплера.
Некоторые планетные системы, включающие несколько планет, демонстрируют резонансные отношения периодов их обращения. В таких случаях применяются дополнительные закономерности, объясняющие резонансные явления.
Таблица 4.1. Некоторые параметры орбитального движения планет солнечной системы
| Планета | Радиус орбиты (а.е.) | Период обращения (земные года) |
| Меркурий | 0.387 | 0.24 |
| Венера | 0.723 | 0.62 |
| Земля | 1 | 1 |
| Марс | 1.524 | 1.88 |
| Юпитер | 5.203 | 11.86 |
| Сатурн | 9.539 | 29.46 |
| Уран | 19.18 | 84.01 |
| Нептун | 30.07 | 164.79 |
Таблица 4.8. Расстояния до планетоидов при их периоде обращения менее 5 лет
| Период обращения (лет) | Среднее расстояние (а.е.) |
| 2 | 2 |
| 2.5 | 2.6 |
| 3 | 3.1 |
| 4 | 3.8 |
| 4.5 | 4.6 |
| 4.8 | 4.9 |
Таким образом, третий закон Кеплера играет важную роль в астрономии и позволяет исследовать движения планет в солнечной системе, а также проводить моделирование орбитального движения экзопланет вне Солнечной системы. Несмотря на причинам его постоянного перестройки в течение истории астрономии, этот закон является одним из наиболее общих и универсальных законов движения небесных тел.
Литература:
1. Тициус-Боде.—Астрономический альманах за 2015 год, стр.171-187.
2. Литература по астрономии.—Альманах астронома и астрофизика 2013 года.

0 Комментариев