Космический полет — одна из величайших технических и научных достижений человечества. На протяжении всей нашей истории мы мечтали о покорении космоса, о поиске ответов на вечные вопросы о происхождении жизни и о смысле нашего существования. И лишь в XX веке, благодаря невероятному развитию науки и технологий, стала возможной реализация этих мечтаний.
Одним из важных понятий, связанных с космическим полетом, является понятие первой космической скорости. Первая космическая скорость – это минимальная скорость, которая необходима для покинуть планету и войти на орбиту вокруг нее. Именно эта скорость позволяет объектам преодолеть силу притяжения Земли и войти на орбиту. В то же время, первая космическая скорость означает и то, что объект движется с такой скоростью, что сила тяготения и центростремительная сила взаимно уравновешивают друг друга.
Чтобы лучше понять значение первой космической скорости, необходимо разобраться в определении орбитального движения. Орбитальное движение представляет собой движение объекта вокруг другого объекта под воздействием их гравитационного взаимодействия. Представьте себе ситуацию, когда человек находится в лифте и нажимает кнопку, чтобы подняться на второй этаж. Когда лифт начинает движение вверх, вы ощущаете ускорение. Если бы вас не удерживали пол и стены лифта, вы бы оторвались от пола и начали бы свободно плавать внутри. Таким образом, чтобы находиться на орбите вокруг Земли, объект должен двигаться с достаточно большой скоростью, чтобы не падать на Землю, но и не улетать в космос за пределы притяжения. Данная скорость, как вы уже поняли, называется первой космической скоростью.
Формулы для расчета первой космической скорости зависят от массы планеты и ее радиуса. В случае Земли, первая космическая скорость примерно равна 7.9 километров в секунду. Однако, для каждой планеты эта скорость будет отличаться в зависимости от ее массы и размеров. Например, ускорение свободного падения на Луне составляет всего 1.6 метров в секунду, поэтому первая космическая скорость для Луны будет гораздо меньше, чем для Земли.
Интересно отметить, что для построения орбиты вокруг планеты необходимо знание не только первой космической скорости, но и других скоростей: второй, третьей и четвертой. Вторая космическая скорость – это скорость, достаточная для того, чтобы объект остался на орбите вокруг планеты. Третья космическая скорость – это скорость, достаточная что объект более не будет вращаться вокруг планеты и начнет двигаться в пространстве по гиперболической (непрерываемой) траектории. Четвертая космическая скорость – это скорость, достаточная для покидания сферы влияния планеты и входа объекта на орбиту вокруг Солнца.
Первая космическая скорость планет солнечной системы
В этом случае, объект движется под действием силы тяжести, которая притягивает его к центру планеты. С увеличением скорости объекта, сила тяжести уменьшается и его траектория становится кривой. Когда скорость становится достаточной, чтобы преодолеть гравитационную силу, объект вступает на орбиту, при которой он может вращаться вокруг планеты без дополнительных полетных правок.
Для расчета первой космической скорости необходимо знать значение ускорения свободного падения на данной планете (g) и радиус планеты (R). Первая космическая скорость (V1) может быть вычислена по формуле:
| V1 = √(2gR) |
Вторая космическая скорость (V2) – это скорость, которая позволяет объекту покинуть планету полностью и войти на орбиту вокруг Солнца. Она рассчитывается по формуле:
| V2 = √(2gR(1 + R/h)) |
где h — это высота объекта над поверхностью планеты.
Таким образом, первая космическая скорость является минимальной скоростью для достижения орбитального движения вокруг планеты, а вторая космическая скорость дает возможность покинуть планету и вступить на орбиту вокруг Солнца.
Зависимость скорости от гравитации
Величина гравитационной силы зависит от массы тела и расстояния между ними. Мы можем использовать уравнение гравитации, чтобы подставив значения массы Земли (5,97 x 1024 кг), расстояния от Земли до некоторой точки в космосе (например, радиус околоземной орбиты 6 371 км) и постоянную гравитации (G ≈ 6,67 x 10-11 Н * м2 / кг2), рассчитать величину силы притяжения к Земле:
| Масса Земли (M) | Расстояние от точки до Земли (r) | Гравитационная постоянная (G) | Сила притяжения (F) |
|---|---|---|---|
| 5,97 x 1024 кг | 6 371 км = 6,371 x 106 м | 6,67 x 10-11 Н * м2 / кг2 | 9,77 x 1020 Н |
Теперь, чтобы понять, какая скорость необходима спутнику или космическому аппарату, чтобы находиться в определенной орбите, мы можем использовать формулу для кинетической энергии:
Ek = (1/2) * m * v2
Где m — масса спутника или космического аппарата, v — скорость.
Мы также можем использовать уравнение для центростремительной силы (сила, действующая на движущееся тело в радиальном направлении) для определения скорости, которую тело должно иметь, чтобы вращаться вокруг Земли на определенном расстоянии от поверхности. Это уравнение выглядит следующим образом:
F = m * aцс
Где F — центростремительная сила, m — масса тела, aцс — центростремительное ускорение.
Можно показать, что центростремительное ускорение (а значит, и центростремительная сила) зависит от скорости и радиуса орбиты:
aцс = v2 / r
Теперь мы можем объединить эти два уравнения и рассчиать зависимость скорости от гравитации:
F = m * aцс
mg = m * v2 / r
v2 = g * r
v = sqrt(g * r)
Где:
m — масса тела,
g — ускорение свободного падения на поверхности Земли (~9,8 м/с2),
r — радиус орбиты относительно центра Земли,
v — скорость.
Таким образом, зависимость скорости от гравитации можно выразить формулой:
v = sqrt(g * r)
Используя эту формулу, можно определить скорость, требуемую для успешного полета спутника или космического аппарата на различных орбитах вокруг Земли или других планет солнечной системы.
Роль энергии в орбитальном движении
Орбитальное движение космических тел в солнечной системе основано на балансе гравитационной силы и кинетической энергии. Возьмем, к примеру, космическую ракету, которая стремится выйти на орбиту Земли.
Для того чтобы покинуть поверхность планеты и двигаться по круговой орбите вокруг нее, ракета должна развить определенную скорость, называемую космической скоростью. Если ракета не разовьет такую скорость, она будет тормозиться гравитационным притяжением и вернется обратно на поверхность Земли. Для выхода на космическую орбиту необходима скорость порядка 7.9 км/с.
Расчет космической скорости основан на основной формуле кинетической энергии. В данном случае, кинетическая энергия ракеты должна быть равна потенциальной энергии, приложенной к телу Землей. Это достигается путем уравновешивания гравитационной силы с космической скоростью в вертикальном направлении.
Величина ускорения, которую испытывает тело в космическом движении, можно вычислить с помощью известной формулы второго закона Ньютона: F = m * a, где F — сила гравитационного притяжения, m — масса тела, а — ускорение.
Существует несколько подходов к расчету силы гравитации:
- По формуле Ньютона: F = G * (m1 * m2) / r^2, где F — сила притяжения, G — гравитационная постоянная, m1 и m2 — массы тел, r — расстояние между ними.
- С учетом разницы высоты: F = (G * M * m) / (R + h)^2 — (G * M * m) / R^2, где M — масса Земли, m — масса тела, R — радиус Земли, h — высота тела над поверхностью Земли.
Для орбитального движения также важно учитывать форму орбиты. В космическом полете наиболее эффективными орбитами являются круговые и конические орбиты. В круговом движении скорость постоянна, а в коническом — меняется.
Итак, энергия играет ключевую роль в орбитальном движении. Она определяет скорость, силу притяжения и форму орбиты. Благодаря правильному расчету энергии и скоростей мы можем достичь космической орбиты и изучать Вселенную внешних искусственным спутников и межпланетных миссий.
Орбитальное движение планет
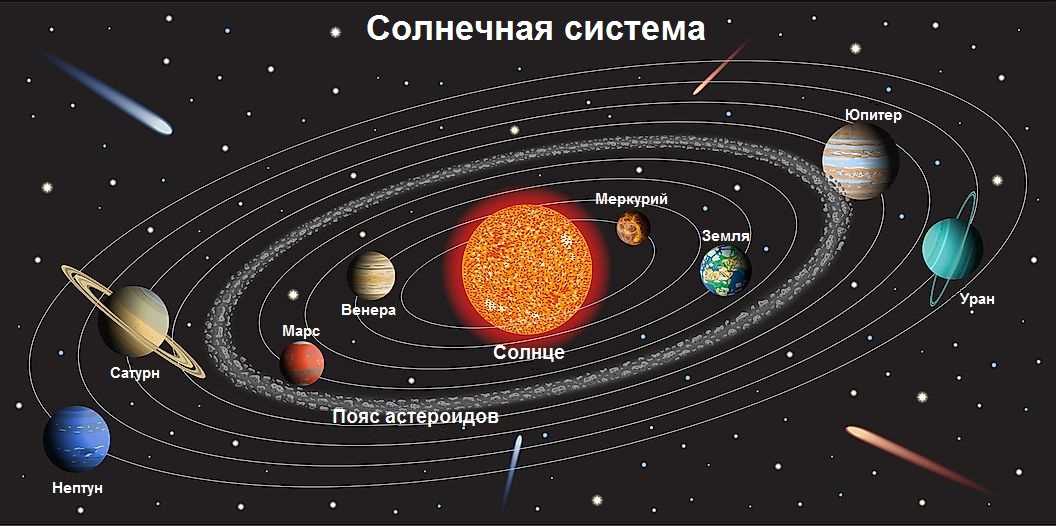
Первая космическая скорость – это скорость, при достижении которой тело сможет войти в состояние круговой орбиты вокруг Земли. Для достижения этой скорости необходимо преодолеть силу тяжести Земли, которая приблизительно равна 10 м/с². Если бы на Земле была достаточная масса и достаточная скорость, чтобы удерживающие троса могли править лифт, телу при скорости 10,2 м/с удавалось бы войти в орбиту. В этом случае просто могло бы быть достигнуто состояние равновесия между силой тяжести и ускорением, вызванным движением по круговой орбите.
Круговая орбита – это орбита, на которой спутник движется вокруг планеты или искусственного тела в солнечной системе. Скорость на такой орбите такова, что спутник испытывает удерживающие силы, достаточные для поддержания его вращения вокруг планеты или искусственного тела.
Орбитальное движение планет является результатом взаимодействия гравитационной силы и массы планеты. Внешние спутники вращаются вокруг своих небесных объектов, таких как планеты, на определенных расстояниях. Радиус этой орбиты и масса объекта определяют период вращения планеты вокруг своего спутника.
Первая космическая скорость и достижение орбиты
Для достижения орбиты планеты необходима первая космическая скорость, которую можно вычислить по формуле:
v = sqrt((G * M) / r)
где:
- v – первая космическая скорость
- G – гравитационная постоянная (примерное значение 6,67 * 10-11 м³/(кг с²))
- M – масса планеты
- r – радиус орбиты планеты
Как только объект достигает первой космической скорости при данной массе планеты и радиусе орбиты, он начинает двигаться по круговой орбите вокруг планеты.
Влияние массы и радиуса орбиты на скорости
Масса планеты и радиус орбиты влияют на первую космическую скорость. Чем больше масса планеты, тем выше первая космическая скорость, необходимая для достижения орбиты. Также, чем больше радиус орбиты, тем ниже первая космическая скорость будет достаточной для достижения орбиты.
Из этого понимается, что для достижения орбиты на малых скоростях требуется радиус большей орбиты или увеличение массы планеты. На практике это означает, что спутники молодой Земли могли вращаться только на больших расстояниях от нашей планеты.
Первая космическая скорость является важным понятием в космической науке и исследованиях. Она играет ключевую роль в достижении орбиты и позволяет спутникам искусственных тел оставаться на орбите вокруг планеты.
Вторая космическая скорость:
Величина второй космической скорости зависит от массы тела и ускорения свободного падения, которое на Земле составляет около 9,8 м/с². Значение второй космической скорости составляет около 7,9 км/с. Это значит, что чтобы достичь орбиты вокруг Земли, тело должно двигаться со скоростью около 7,9 км/с.
Вторая космическая скорость также может быть выведена с помощью формулы, где В — вторая космическая скорость, G — ускорение свободного падения, а R — радиус Земли:
В = √(G∗R)
Такое значение скорости позволяет телу уйти за пределы атмосферы Земли и остаться на орбите. При этом, если скорость ниже второй космической скорости, то тело будет опускаться обратно на Землю под действием силы тяжести.
Испытывая действие ускорения свободного падения на поверхности Земли, тело находится под действием сил тяжести, которые удерживают его на Земле. Если мы постреляем тело из пистолета с массой m, то результатом действия этой силы тяжести на тело будет его вес mg, где g — ускорение свободного падения.
Внешние по отношению к телу силы удерживают его в состоянии покоя или движения с постоянной скоростью. Но если начать действовать на тело силами, увеличивающими его скорость, то тело будет двигаться по криволинейной траектории в результате действия составляющих его сил.
Это состояние называется искусственным спутниковым движением, а траектория, по которой движется тело, имеет форму эллипса, концентрического с Землей. Это орбита, и такую орбиту тело будет описывать, если его скорость будет равна второй космической скорости.
Знаем, что значение второй космической скорости составляет около 7,9 км/с. Результатом действия такой скорости на тело является та центростремительная сила, которая увлекает тело вдоль поверхности Земли, создавая его вес.
Математическое определение
Для расчета первой космической скорости планеты солнечной системы необходимо учитывать притяжение гравитации, энергию и орбитальное движение тел. Основная формула, которую можно использовать для этого, приведена ниже:
| Номер | Формула | Описание |
|---|---|---|
| 1. | v = √(2GM/r) | Формула для расчета первой космической скорости |
В этой формуле G — гравитационная постоянная, M — масса планеты, r — радиус планеты. Коэффициент 2 в числителе используется, чтобы учесть опору против движения вниз.
Достаточная скорость, чтобы покинуть землю и войти в космическую орбиту, известна как первая космическая скорость. Именно эта скорость позволяет объекту преодолеть притяжение Земли и войти в космос.
Для расчета первой космической скорости используется эта формула и входные данные, такие как масса и радиус планеты. После подстановки значений формула позволяет найти скорость, которую объект должен иметь, чтобы преодолеть силу притяжения планеты и войти в космическую орбиту.
Примечания:
- Ускорение свободного падения g = 9,8 м/с2.
- Для земли mg = G*M*m/r2.
- Формула также применима для расчета первой космической скорости спутника (на рассмотренном круговом движении выше поверхности Земли).
- В случае орбиты необходимо использовать другую формулу для расчета. Например, для эллиптической орбиты формула будет выглядеть следующим образом: v = √(GM*(2/r — 1/a)), где a — большая полуось эллипса.
Расчет первой космической скорости позволяет получить значимую величину для дальнейших исследований и экспериментов в космической системе. Это также является основой для расчета новых скоростей и орбит в системе планет солнечной системы.
Примеры планет с второй космической скоростью
Вторая космическая скорость – это минимальная скорость, при которой объект может двигаться в космическом пространстве вокруг планеты, не падая на ее поверхность. Формула для расчета второй космической скорости очень похожа на формулу для первой космической скорости, но с некоторыми приложенными изменениями. Если первая космическая скорость, удерживающая объект в круговой орбите вокруг Земли, составляет около 7,9 км/с, то вторая космическая скорость рассчитывается с помощью следующей формулы:
v = sqrt((2 * G * M) / r)
где:
- v — вторая космическая скорость
- G — гравитационная постоянная (approximately 6.67 x 10-11 м3 / кг / с2)
- M — масса планеты
- r — расстояние от центра планеты до объекта
Таким образом, вторая космическая скорость зависит от массы планеты и расстояния от ее центра до объекта. Чем больше масса планеты и меньше расстояние, тем выше будет вторая космическая скорость.
Давайте рассмотрим примеры планет с второй космической скоростью:
- Земля — вторая космическая скорость на Земле составляет около 11,2 км/с. Это означает, что если объект движется со скоростью больше 11,2 км/с, он сможет уйти в космическое пространство и больше не вернуться к Земле.
- Марс — вторая космическая скорость на Марсе составляет около 5 км/с. Это значит, что для покидания Марса и входа в космическую орбиту объекту необходимо достичь скорости более 5 км/с.
- Юпитер — вторая космическая скорость на Юпитере составляет около 59,5 км/с. Это очень большая скорость, необходимая для покидания планеты и входа в космическое пространство.
Примечания: значения второй космической скорости для различных планет могут варьироваться в зависимости от точного значения массы планеты и ее радиуса.

0 Комментариев