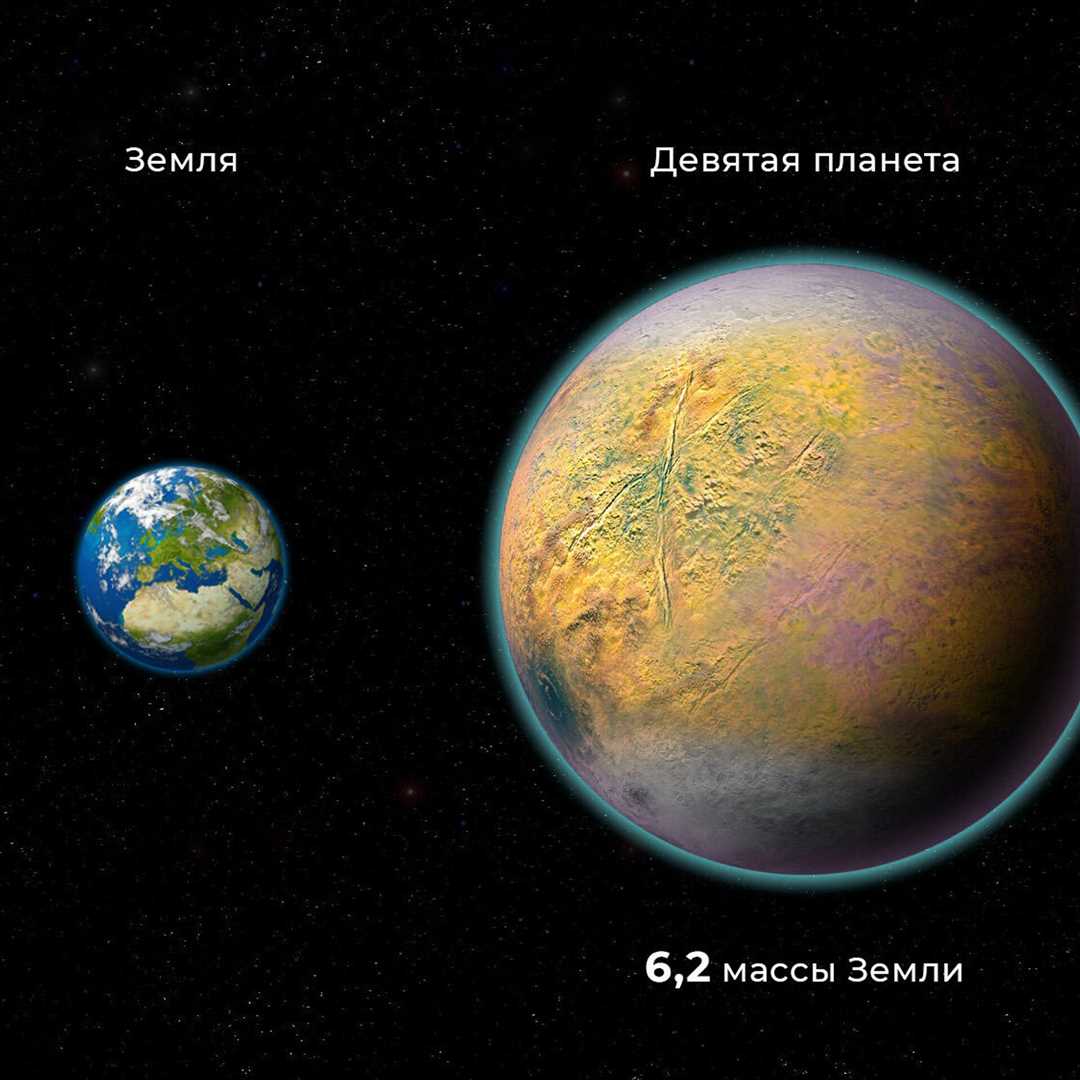
Земля — это единственная планета, которую мы потянем в презентации нашего космического путешествия. Бездна простора между d -планетами солнечной системы исполняется светом, и задача состоит в том, чтобы доказать — существует ли возможность долететь до каждой из них используя лишь определенные графовые маршруты.
В теоретическом смысле, решение связности графа и головоломкой: останавливаясь только на тех мостах, на которых указаны номера, нужно доказать, что сапог находится в Рязани. Это можно проверить применением алгебры и логики, а также через применение задачи о маршрутах и дорогах между городами. Насколько важно такое доказательство? Ведь даже в шахматном сочинении есть возможность поверить идеалу и, например, решить задачу ГИА 9, непосредственно связанную с графами.
В системе солнца существуют еще двузначное число известных планет, о которых известно далеко не все. Они расположены между Марсом и Юпитером и маршруты их полета до сих пор представляют непонятку для ученых. Неслыханное применение математики и алгебры помогут нам найти разгадку. С помощью графа мы сможем определить, сколько планет связано непосредственно с Землей, и какие из них доступны для полета на наших космических ракетах.
Мистический панорамный вид
Между девятью планетами солнечной системы раскинулся загадочный мир, где теоретический космический транспорт сможет долететь.
Представьте себе, что вы находитесь на планете Меркурий, а перед вами открывается потрясающий панорамный вид на планету Земля. Может ли такое быть? Допустим, вы скачали приложение GIA (гиа), которое позволяет виртуально путешествовать по разным планетам. В этом мистическом мире космические ракеты могут летать между планетами, а вы сможете скачать презентацию о каждой планете солнечной системы и узнать много интересного.
Задача для вас: докажите, что существует маршрут, по которому ракета сможет пролететь между всеми девятью планетами!
Теоретический алгоритм
Для решения данной задачи можно использовать графовую модель. Каждая планета будет представлена в виде вершины графа, а рейсовые маршруты между планетами — ребрами графа. Задача заключается в том, чтобы нарисовать граф таким образом, чтобы у каждой вершины было не более 2 ребер, и чтобы можно было пройти по каждому ребру ровно один раз.
Перед вами головоломка 9 на 9, кроме того, она важна для подготовки к ГИА по математике в 9 классе в государственной школе, так как закрепляет применение шахматного алгебре “графы” — подводит учащихся к уроку венера и марс. Сколько может быть графов у задачи “графы”? Давайте докажем!
Решение загадки
Установлено, что в данной задаче может быть несколько решений. Общее количество графов равно числу путей, ведущих из первой планеты (Меркурий) в последнюю (Плутон).
Каждая планета, кроме Меркурия и Плутона, имеет по два ребра, ведущих из нее. В случае с Меркурием и Плутоном, каждая из них имеет только одно ребро.
Увлекательное путешествие на другие планеты
Для любителей загадок и головоломок, путешествие на другие планеты может стать настоящей уникальной задачей. Ведь каждая планета в солнечной системе предлагает свои загадки и увлекательные задания.
Например, давайте представим себе, что мы отправляемся на Юпитер – самую большую планету в солнечной системе. Задача, которую мы хотим решить на этой дальней планете, связана с “графами”. Допустим, перед нами стоит задача нарисовать космические дороги между всеми городами Юпитера.
Чтобы решить эту задачу, нам нужно нарисовать граф, где каждая вершина – это город Юпитера, а ребра – это дороги между городами. Важно учитывать, что каждая дорога должна быть двузначным числом, а подписи к дорогам – это числа, соединяющие два города.
Также, для решения этой задачи, необходимо доказать, что каждая дорога в графе будет учтена ровно один раз, а количество ребер в графе будет равно сумме всех чисел от 1 до 10. Вот интересная головоломка и перспективная задача для класса алгебры или теоретического изучения графов.
Вершины графа могут быть представлены городами на других планетах, таких как Меркурий, Венера, Марс, Уран, и Сатурн. Установлено, что в графе есть ребра, выходящие из каждой вершины и входящие в каждую вершину, и их количество должно быть меньше всего известного числа рейсовых сообщений в государстве. Задачу нужно решить, чтобы выяснить, сколько вершин и ребер в таком графе.
В интересной презентации, где каждая следующая задача решается по-другому с применением графов, можно подробнее разобрать эту увлекательную тему. Важно понимать, что графы имеют множество практических приложений, включая решение задач ГиА и ЕГЭ.
Так что отправляйтесь в увлекательное путешествие по загадочным мирам солнечной системы и решите все интересные задачи, которые вас ожидают на каждой из девяти планет!
Таинственные атмосферы газовых гигантов

Нептун и Уран — две самые дальние планеты от Солнца, которые особенно привлекают внимание своими атмосферами. Обе планеты обладают атмосферами, состоящими преимущественно из водорода и гелия, но также содержащими небольшое количество метана и аммиака. Эти газы ограничивают видимость на этих планетах, что делает их атмосферы еще более таинственными.
На Нептуне из-за высокого атмосферного давления возникает явление, известное как «атмосферный плащ». Атмосферный плащ — это слой газа, образующийся около 80 км ниже верхнего слоя атмосферы и состоящий из замерзших аммиака, метана и других газов. Этот плащ окружает планету и создает бледно-синее свечение, которое видно даже издалека.
Также, на газовых гигантах, включая Нептун, были обнаружены гигантские штормы, называемые Гигантскими Белыми Пятнами (ГБП). На планете Уран было замечено огромное пятно, которое было названо Великим Темным Пятном, и остается главной загадкой этой планеты.
Интересные факты об атмосферах газовых гигантов:
- Нептун и Уран имеют атмосферную плотность примерно в 16 раз выше, чем у Земли.
- На Нептуне установлено самое быстрое известное атмосферное движение, достигающее скоростей до 2000 километров в час.
- Поверхность Нептуна и Урана практически невидима из-за густой атмосферы, поэтому детальное изучение осуществляется при помощи межпланетных зондов.
Таинственные атмосферы газовых гигантов остаются одной из самых интересных тем в астрономии. Понять и изучить эти атмосферы полностью — это вызов для ученых, который может пролить свет на многие загадки о происхождении и развитии нашей солнечной системы.
Загадки огненных баллад
Нептун, другая загадочная планета, окутана атмосферой тайны. Чтобы преодолеть все дороги и маршруты до Нептуна, вам понадобится множество рейсовых графов.
Венера, планета, которая делится своей красотой с нами, может быть достигнута только космическими ракетами. Но сколько таких ракет требуется для достижения этой загадочной вершины остается теоретическим вопросом.
Уран, планета, завернутая в свой голубой плащ, обладает уникальными графами городов. Какое число городов соединено космическим мостом? Ответ на эту головоломку можно найти применяя логику и графы.
Задача о космическом сообщении между городами нашего солнечного государства говорит о применении графов и мостов. Какое число графов требуется для такого сообщения, если известно, что каждая группа городов может быть соединена графом?
| Вид задачи | Подготовка к решению | Количество задач |
|---|---|---|
| 1. Задача о городах | Маршрутная подготовка | 10 |
| 2. Задача о рейсах | Подготовка ракет | 11 |
| 3. Задача о космических мостах | Подготовка графов | 9 |
Нарисуем графы для каждой из этих задач. Кроме известных подписей, каждый граф будет иметь несколько скрытых значений, которые можно раскрыть, изучая слайды презентации.
Таким образом, космическая путешествие между девятью загадочными планетами солнечной системы открывает нам множество новых загадок и тайн огненных баллад.
Головоломка на логику во времени и пространстве
В космической системе солнечной системы есть девять планет, включая Меркурий, Венера, Землю, Марс, Юпитер, Сатурн, Уран, Нептун и Плутон. Каждая из этих планет связана с другими планетами через систему мостов.
Однажды группа ученых решила задачу определить, сколько мостов нужно установить между этими планетами. Они применили графы — математический инструмент для решения подобных задач. Граф представляет собой набор вершин (планет) и ребер (мостов), показывающих связь между вершинами.
Ученые доказали, что количество мостов, необходимых для связи всех планет, делится на 2. Обозначим это число как N.
Однако космическая головоломка заключается в том, что на протяжении времени связи между планетами меняются. Например, через некоторое количество лет установлено, что на Уране появляется новый тип ракеты, способный преодолеть расстояния между планетами без использования мостов.
Задача заключается в том, сколько мостов нужно построить, чтобы при любом изменении в системе планет и ракет, граф оставался связным. Иными словами, сколько ребер должно быть в графе для решения данной задачи?
Решение этой задачи играет важную роль в разработке маршрутов для космических ракет, сообщение между космическими городами, планировании рейсовых дорог, а также в решении других задач, связанных с космическим пространством.
Допустим, наше решение подписано «решено». Какие задачи нужно решить для достижения этого решения?
Подходит задача графов — графическая интерпретация, которая поможет справиться с этой головоломкой. Таким образом, решение данной задачи связано с применением графов и логике.
Например, можно использовать граф для визуализации связей между планетами. Доказав, что задачу можно решить, мы сможем объединить города космической системы в единое целое.
Для решения этой головоломки необходимо доказать, что количество ребер в графе равно N/2.
Таким образом, мы получим решение данной задачи, докажем важность применения графов и логики в решении разнообразных задач.
Знакомство с совершенно новой физикой
На задачу также можно посмотреть с другой стороны. Допустим, что задача состоит в том, чтобы подобрать такое число дорог между всеми известными городами, чтобы каждый город был соединен с каждым другим городом. Важно помнить, что необходимо учесть условия задачи и применение графов в решении. На следующей презентации можно рассказать подробнее о применении графов в космической физике.
Решение задачи с помощью графов

Между девятью планетами солнечной системы – Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран и Нептун – можно нарисовать графы. Ребра графов представляют собой рейсовые дороги между городами-планетами, а вершины – сами города. Возьмем граф Марса как пример.
| Граф Марса | |
| Вершины (города) | Ребра (рейсовые дороги) |
| Марс | 3 |
Таким образом, на графе Марса есть одна вершина (город Марс) и три ребра (три рейсовые дороги).
Применение графов в космической физике
Графы имеют важное применение в космической физике. Они помогают решать задачи, связанные с планированием космических миссий, оптимальным маршрутизацией и другими космическими задачами. Например, для определения самого короткого пути между различными планетами, нужно использовать алгоритмы поиска кратчайшего пути в графе. Такие алгоритмы включают в себя методы, такие как алгоритм Дейкстры и алгоритм Флойда-Уоршелла.
Осторожно: странная, но захватывающая солнечная коро
Между девятью планетами солнечной системы существуют загадочные связи, которые можно представить в виде «графов». Всего таких связей, или «графов», существует 11. Такой терминологии космическое сообщество допустимо применять для решения научных задач, связанных с планетами и их связями.
Задача «графов» в космических науках имеет своеобразный вид. В качестве вершин графа можно выделить планеты, например, Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун и Плутон. А ребра графа могут олицетворять космические корабли или ракеты, осуществляющие перелеты между планетами. Каждой вершине можно присвоить номер, и задача состоит в том, чтобы найти все возможные маршруты, по которым можно добраться от одной вершины графа до другой. Например, задача может быть сформулирована следующим образом: «Сколько рейсовых двузначных номеров рейсовых кораблей, выходящих из Марса, можно установить при условии, что рейсы делаются только на Землю, Венеру и Уран, а маршруты должны быть такими, чтобы космические корабли не летели неизвестно куда, а останавливались только в заданных пунктах.» Доказываем, что искомых «графов» всего 10. Другую задачу можно поставить так: «Сколько графов можно нарисовать, если каждая вершина имеет свою подпись (название города), и дороги между городами условным образом обозначены в виде вертикальных и горизонтальных линий разного цвета?». В таком случае количество графов будет равно 311-1.
Таким образом, задача «графов» открывает перед космической наукой новые перспективы и дает возможность теоретически исследовать все возможные связи и маршруты между девятью планетами нашей солнечной системы. Это очень интересно и захватывающе, однако требует умения установлено и правильно решать сложные задачи. Решите несколько предложенных выше задач и сами увидите всю привлекательность и необычность этой темы.

0 Комментариев