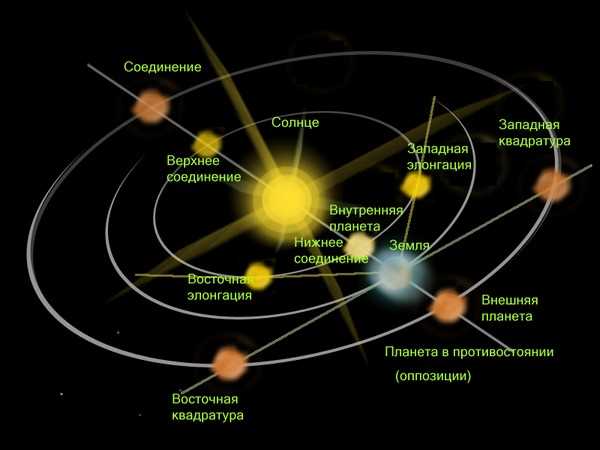
Изучение законов движения планет солнечной системы является одним из фундаментальных направлений современной астрономии. С помощью этих законов мы можем узнать, как планеты солнечной системы эволюционируют и развиваются, как взаимодействуют между собой и с солнцем.
Основанием для изучения законов движения планет является гармонический характер их движения. Все планеты солнечной системы движутся по орбитам, образующим эллипсы. Солнце находится в фокусе эллипсов, а радиус-вектор, соединяющий планету и солнце, описывает равные площади за равные промежутки времени. Это известный закон Кеплера, который называют первым законом движения планет.
Второй закон Кеплера утверждает, что скорость планеты при движении по орбите не является постоянной, а изменяется в зависимости от положения планеты на орбите. Ближе к солнцу планета движется быстрее, а дальше от солнца – медленнее. Это обусловлено влиянием силы тяжести солнца на планету.
Орбита планет: форма траектории и ее характеристики
Эллипс — это геометрическая фигура, которая имеет форму закрытой кривой линии. В природе мы часто встречаемся с такими объектами, как яйца, глаза, листья, их форма также близка к эллипсу. Именно характеристики эллипса определяют форму орбит планет.
Форма эллипса может быть описана такими параметрами, как большая и малая полуоси, эксцентриситет и фокусное расстояние.
Большая полуось (a) — это расстояние от центра эллипса до одного из его фокусов. Это расстояние равно половине большой оси эллипса. Малая полуось (b) — это расстояние от центра эллипса до точки на его границе, перпендикулярной большой оси. Используя эти два параметра, можно определить и другие характеристики эллипса, такие как фокусное расстояние и эксцентриситет.
Эксцентриситет (e) — это число, которое характеризует форму эллипса и определяется следующей формулой: e = √(1 — (b^2 / a^2)). Анализируя эту формулу, можно заключить, что чем меньше эксцентриситет, тем более округлым будет эллипс.
Фокусное расстояние (c) — это расстояние от центра эллипса до фокуса. Оно определяется формулой: c = e * a.
Интересно отметить, что все эллипсы с одним и тем же значением эксцентриситета имеют одинаковую форму, но разные размеры. Это означает, что орбиты разных планет могут быть эллипсами с разными размерами полуосей, но в одной солнечной системе все они будут иметь один и тот же эксцентриситет. Кроме того, в изменяющихся условиях движения планет может происходить эволюция формы орбиты.
Одним из наиболее известных законов движения планет является закон Кеплера, который описывает движение планет и других небесных тел. Согласно этому закону, площадь, охваченная радиус-вектором планеты, за равные промежутки времени, всегда будет одинаковой. Таким образом, скорость планеты меняется во время движения, чтобы поддерживать это соотношение.
Расчет гармонических соотношений между радиус-вектором и угловой скоростью планеты позволяет определить моменты, когда планеты находятся в своих положениях на орбите. Это позволяет прогнозировать будущие положения планет и предсказывать их движение. Все эти соотношения были открыты Йоганном Кеплером в 17 веке и описаны в его законах.
Движение планет вокруг Солнца также влияет на движение спутников. Лунные спутники, например, движутся вокруг своих планет по эллиптическим орбитам, подчиняясь аналогичным законам движения, как и планеты вокруг Солнца. Влияние силы притяжения планеты на спутник приводит к изменению его орбиты и взаимодействию между планетой и спутником.
Всемирный поиск эллиптических орбит и их характеристик продолжается по сей день. Современные методы и технологии позволяют узнавать все больше и больше орбит планет, спутников и других небесных тел. В этом постоянном развитии и поиске новых фактов о нашей солнечной системе необходимо использовать все доступные источники информации и литературы, чтобы расширить наши знания и понимание этого удивительного явления природы.
- Орбиты планет обладают эллиптической формой и характеристиками.
- Форма эллипсов орбит определяется параметрами, такими как большая и малая полуоси, эксцентриситет и фокусное расстояние.
- Орбиты планет могут эволюционировать и менять свою форму в процессе движения.
- Закон Кеплера описывает движение планет и других небесных тел и позволяет прогнозировать их положения на орбите.
- Движение планет также влияет на движение спутников, таких как лунные спутники.
- Всемирный поиск орбит и их характеристик продолжается, чтобы расширить наше понимание солнечной системы.
Примечания:
- В данной статье используются термины и понятия, связанные с астрономическими и геометрическими концепциями. Для более подробной информации рекомендуется обратиться к соответствующей литературе и источникам.
- Таблица найденных значений параметров орбит планет и спутников доступна в специализированных источниках.
Литература:
- Стивен Хокинг. «Краткая история времени».
- Карл Саган. «Космос».
- Астрономические ежегодники и справочники.
Скорость планет на орбите и ее изменения в разных точках

Основные принципы движения планет вокруг Солнца включают в себя такие моменты:
1. Первый закон Кеплера
- Планеты движутся по эллипсам с Солнцем в одном из фокусов.
- Эллипсы, описываемые планетами, могут быть более или менее сплюснутыми в зависимости от склонения орбиты.
2. Второй закон Кеплера
- Радиус-вектор, проведенный из Солнца к планете, описывает равные площади за равные промежутки времени.
- Скорость планеты на орбите меняется, чтобы сохранять эту закономерность.
- На периодах орбиты планеты находятся ближе к Солнцу, и их скорости увеличиваются.
- В перигелии, когда планета находится на наименьшем расстоянии от Солнца, она движется с наибольшей скоростью.
- В афелии, когда планета находится на наибольшем расстоянии от Солнца, она движется с наименьшей скоростью.
Для всех планет симметричным основанием эллиптической орбиты является Солнце. В случае спутников, таких как Луна, симметричным основанием является центр масс системы Земля-Луна.
Эти законы также применимы к другим небесным телам, включая экзопланеты. Кеплеровы законы дали возможность более точно изучить движение планет и других тел в солнечной системе и за ее пределами.
Изменение скоростей планет на орбите имеет большое значение при изучении их траекторий и положения в разные моменты времени. Это позволяет определить моменты, когда происходит наиболее приближение или удаление планеты от Солнца.
Закон равных площадей: равные времена прохождения сканируемой планетой
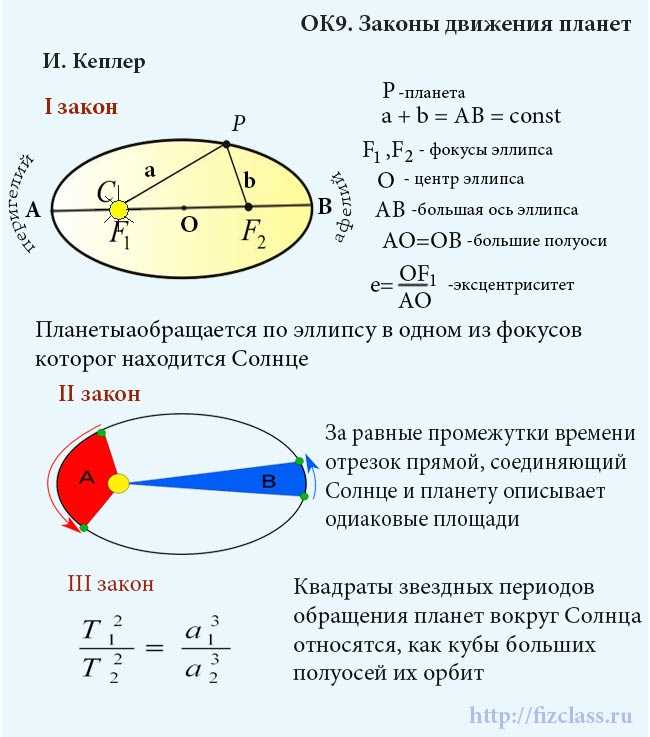
Первый из законов Кеплера гласит, что орбиты планет представляют собой эллипсы, в фокусах которых находится Солнце. Также известно, что скорость планеты в различных точках ее орбиты различна.
Закон равных площадей, или второй закон Кеплера, говорит о том, что радиус-вектор, проведенный от Солнца к планете, за равные промежутки времени сканирует равные площади.
Этот закон означает, что в различные моменты времени скорость планеты изменяется, но площадь, протащенная радиус-вектором за равные промежутки времени, остается постоянной.
Чтобы лучше понять этот закон, можно представить себе планету, движущуюся по эллипсу вокруг Солнца. Вводится точка, находящаяся в определенном расстоянии от Солнца, называемая фокусом. Второй фокус находится в другой точке эллипса. Планета перемещается по орбите таким образом, что скорость движения меняется, но закон равных площадей говорит о том, что сканированные площади от фокуса до точек орбиты симметричны. Таким образом, площади под радиус-вектором, проведенным в разные моменты времени, будут одинаковыми.
Этот закон имеет практическое применение при изучении движения планет и других космических тел. Он позволяет предсказать дальнейшее движение планеты и определить ее местоположение в будущем или в прошлом. Также закон равных площадей помогает понять эволюцию и развитие системы планет, спутников и других тел, движущихся по орбитам вокруг Солнца.
Закон Кеплера о радиусе вектора: особенности движения планет по орбите
Первый закон Кеплера, также известный как закон орбит, утверждает, что орбиты планет являются эллипсами, в одном из фокусов которых находится Солнце. Это означает, что планеты движутся по овалу, а не по кругу.
Второй закон Кеплера, известный как закон радиуса вектора или закон времени равных площадей, говорит нам о том, что скорость планеты на разных участках ее орбиты неодинакова. Он утверждает, что планета движется с максимальной скоростью ближе к Солнцу (в перигелии – точка орбиты, ближайшая к Солнцу) и медленнее в отдалении от Солнца (в апогелии – точка орбиты, наиболее удаленная от Солнца).
Закон радиуса вектора связан с вторым законом Ньютона о гравитации и законом сохранения импульса. Под воздействием гравитационной силы Солнца, планета получает импульс, который под влиянием Закона сохранения импульса приводит к изменению скорости планеты. Это приводит к тому, что планета движется быстрее ближе к Солнцу и медленнее в отдалении от Солнца.
Такие особенности движения планет по орбите позволяют законам Кеплера быть применимыми к многим другим системам во Вселенной. Эти законы имеют гармонический характер и поэтому легко расчетны. Именно благодаря этим законам мы можем описывать и предсказывать движение планет, а также рассчитывать такие моменты, как перигелия, склонение орбиты и другие эволюционные характеристики.
Применение закона Кеплера о радиусе вектора есть также в законе Гари. Закон Гари утверждает, что орбиты планет солнечной системы сохраняют свою форму и ориентацию в промежуток времени. Силой, которая обусловливает сохранение орбиты, является гравитационное влияние других планет и Солнца.
Таким образом, законы Кеплера о радиусе вектора позволяют лучше понять особенности движения планет по их орбитам вокруг Солнца. Они объясняют, почему планеты движутся по эллиптическим орбитам, а также как скорость планеты меняется в зависимости от расстояния от Солнца. Эти законы, установленные Иоганном Кеплером, имеют широкое применение и позволяют нам лучше понять и предсказывать движение планет и других небесных объектов во Вселенной.
Планета и ее солярные сутки: скорость вращения вокруг своей оси

Скорость вращения планеты может быть разной для разных планет. Например, Земля вращается со средней скоростью около 1670 километров в час. В то же время, планета Юпитер вращается намного быстрее, со скоростью около 45000 километров в час. Некоторые планеты, такие как Венера, вращаются в обратном направлении, из-за чего их солярные сутки длительнее, чем период их обращения вокруг Солнца.
Скорость вращения планеты вокруг своей оси зависит от ее положения в орбите. Иногда планеты достигают наибольших скоростей вблизи перигелия, то есть вблизи той точки своей орбиты, где они находятся ближе всего к Солнцу. В других случаях, скорость вращения может быть максимальной вблизи афелия, самой удаленной точки от Солнца на орбите.
Такие различия в скоростях вращения планет объясняются взаимодействиями силой тяжести и гравитационной притяжением Солнца. В результате этих взаимодействий орбиты планет и их траектории эволюционируют с течением времени.
Одним из основных законов движения планет является закон гармонических движений, сформулированный Кеплером в 17 веке. Этот закон описывает закономерности движения планет по их орбитам, а также изменение их скоростей во времени.
Кеплером был установлен закон сохранения энергии для планет, согласно которому сумма кинетической и потенциальной энергии планеты остается постоянной на протяжении всего ее движения. Таким образом, при изменении скорости планеты в одном месте ее орбиты, скорость в другом месте будет изменяться таким образом, чтобы обеспечить сохранение полной энергии.
Эта закономерность движения планет и эволюция их орбит практически равносильны в обратновремени. Это означает, что планеты могут эволюционировать как в одном, так и в другом направлении, в зависимости от начальных условий и характеристик их орбит.
Соответствующий расчет скоростей и положений планет в зависимости от времени можно произвести с использованием уравнений движения и таблицы соответствующих расстояний и периодов обращения планет.
Описывая движение планет в солнечной системе, можно отметить, что планеты движутся внутри своих орбит сравнительно медленнее комет и других космических тел. Небольшие изменения в скорости и склонении орбит могут происходить под влиянием гравитационного взаимодействия с другими планетами и космическими телами.
Всемирного значения приобрел первый закон Кеплера, устанавливающий роль Солнца в описании движения планет. Согласно этому закону, Солнце занимает одну из двух фокусов овала, по которому движется планета. Этот закон был получен Кеплером на основе эмпирических данных и стал важным шагом в понимании структуры солнечной системы. Более подробные вычисления и описания орбит планет, а также изменение их параметров во времени и пространстве осуществляются с использованием более точных методов, основанных на законах ньютоновской механики.
Таким образом, скорость вращения планет вокруг своей оси играет важную роль в эволюции планет и их орбит. Изменение скоростей планет приводит к изменению их орбиты и движения в космическом пространстве.
Взаимодействие планет и гравитационные силы: их влияние на движение планет

Движение планет солнечной системы определяется взаимодействием планет с силами гравитации.
Когда планеты движутся вокруг Солнца, у них практически постоянны направление и скорость. Они описывают овалы, которые называются эллипсами, с Солнцем в одном из фокусов эллипса.
Гравитационная сила, действующая на планеты, обращается к центру Солнечной системы. Планеты влияют друг на друга и на Солнце своими гравитационными силами. Из-за этого, их траектории могут быть немного искривлены.
Идея о гравитационном взаимодействии была введена в науку в XVII веке Йоханном Кеплером и сформулирована в виде трех законов Кеплера.
Первый закон Кеплера, также называемый законом эллипсов, утверждает, что все планеты движутся по эллипсу, где Солнце находится в одном из фокусов эллипса.
Второй закон Кеплера утверждает, что скорость, с которой планета движется вокруг Солнца, изменяется во время ее орбиты. Он показывает, что планеты движутся быстрее, когда они находятся ближе к Солнцу, и медленнее, когда они находятся дальше от Солнца.
Третий закон Кеплера, называемый «гармоническим законом», связывает период обращения планеты вокруг Солнца с расстоянием до Солнца. Он говорит нам, что квадрат периода обращения планеты пропорционален кубу расстояния от планеты до Солнца.
Эти законы Кеплера позволяют нам описывать движение планет и предсказывать их положение в будущем. Они также позволяют нам лучше понять природу вселенной и ее эволюцию.
Исторически, эти законы Кеплера были открыты во время исследования орбит планет, но они также применимы к движению других тел во Вселенной, таких как спутники и кометы.
Мы также можем использовать законы Кеплера для планирования космических миссий и вычисления орбит и траекторий космических аппаратов.
Взаимодействие планет и гравитационные силы играют важную роль в эволюции Солнечной системы и всей Вселенной. Эти силы всегда присутствуют и влияют на движение планет, позволяя нам лучше понять устройство вселенной и ее закономерности.

0 Комментариев